Mathematische Beispiele
Willkommen Auf der Веб -сайт
Mathexample.com
Diese BildungSressource IST Für Den Erwerb undWicklung Praktischer Mathematisher 44. Für Erwerb undwicklung Praktischer .
“Die Drei und die Sieben sind die beiden größten geistigen Zahlen ”
~Honore de Balzac
Website-Ziele:
- 0022
- praktische Erfahrung in der Lösung mathematischer Aufgaben sammeln
- Steigerung der Geschwindigkeit und Qualität des logischen und mathematischen Denkens
- Entwicklung von Gedächtnis, Achtsamkeit und Konzentration
Mit dieser Ressource können Sie:
- Grundkenntnisse in Adding, Subtraktion, Multiplikation und Division erwerben
- Lernen Sie die Multiplikationstabelle mit praktischen Übungen
- Aktion mit ganzen Zahlen, Dezimal- und Bruchzahlen lernen
- Beherrsche die Methoden zum Lösen von Gleichungen
- lerne Wörter Richtig zu buchstabieren
Die Site beetet die folgenden Funktionen:
Die Fähigkeit, рациональное zu denken , muss entwickelt und gefestigt werden, es ist einfacher, mit uns zu tun!
10+
Erstellen Sie Blätter mit mathematischen Beispielen für die Division durch eine Spaltenmethode . Die Zahlen eines Beispiels sind ganze Zahlen . Die Antworten sind immer positiv и ganzzahlig . Insgesamt 1 Variante и 5 Komplexitätsstufen.
Divisor
Erstellt Beispiele mit einer Divisionsoperation von Ganzzahlen durch eine Spaltenmethode
1 Variante 5 Ebenen
Variante: 1 Ebene: Einfach
12+
Erstellt Arbeitsblätter mit englischen Infinitiven , in denen einige Вертер Фелен. Fehlende Verben müssen vervollständigt werden. Нур 3 Optionen и 3 Schwierigkeitsgrade.
Infinitiv
Erstellt Arbeitsblätter mit englischen Infinitiven , in denen einige Wörter fehlen, fehlende Verben ausgefüllt werden müssen
3 Varianten 3 Ebenen
| waylay | waylaid | ||
| typecast | typecast |
Вариант: 1 Ebene: Schwierig
8+
Tägliche Multiplikationsübungen. Entwickelt die Fähigkeit, Beispiele mit der Multiplikationsoperation zu lösen.
Multiplikation #9
| 5 × 6 = | 3 × 3 = | 5 × 7 = |
Versuche: 3 Ebene: Einfach 9000
.10129
. die Subtraktion и Addition mit einer Spaltenmethode . Antworten und Zahlen eines Beispiels sind ganzzahlig и положительный . Insgesamt 3 Varianten und 3 Komplexitätsstufen.
Spalte
Erstellt Beispiele für die Addition oder Subtraktion von Ganzzahlen durch eine Spaltenmethode
3 Varianten 3 Ebenen
|
|
|
Вариант: 3 Ebene: Hart
9+
Erstellen Sie Blätter mit linearen Gleichungen .
Необычный автосалон
Один автосалон купил подержанную машину за 450 тысяч и через неделю продал её за 525 тысяч. Директор салона решил, что такая модель пользуется спросом, так что он дал менеджерам задание — найти ещё одну подобную машину. Они нашли такую же за 550 тысяч, купили её, но директор повёл себя странно. Он снова поставил на неё ценник в 525 тысяч, и машина ушла за два дня. Помогите бухгалтерии понять, заработал в итоге салон или потерял часть денег?
У этой задачи три решения: интуитивное, пошаговое и бухгалтерское. Сравните подходы.
Многие решают эту задачу так:
- Было 450 тысяч.
- Купили машину и продали за 525 тысяч.
- После продажи заработали 75.
- Взяли в долг 25.
- Купили вторую машину и продали снова за 525.
- Изначально было 450, стало 525, значит, прибыль снова составила 75 тысяч, а общая — 150 тысяч.
- Отдаём 25 долга, получаем прибыль 125 тысяч.
Но это неправильно. Правильно — ниже.
Давайте разберём эту сделку по шагам, чтобы понять, сколько денег было у салона на каждом этапе.
В самом начале у них было 450 тысяч — запомним это. Эти деньги пошли на покупку первой машины, поэтому на втором шаге у салона стало 0 рублей, но появился автомобиль.
На третьем шаге его продали за 525 тысяч, которые и ушли в кассу. Пока прибыль салона равна: 525 − 450 = 75 тысяч.
Вторая машина стоила на 25 тысяч дороже, чем у них было — 550, поэтому салон взял в долг 25 тысяч и купил её (шаг номер четыре). Здесь прибыль салона исчезла и появился убыток в 25 тысяч.
Пятым шагом они продали вторую машину за 525 тысяч, положили деньги в кассу и стали разбираться с долгами. После того как они вернули сумму, которую были должны, у салона осталось 500 тысяч, а начинали они с суммы в 450 тысяч. Получается, что они заработали 500 − 450 = 50 тысяч.
Бухгалтеры работают так: считают все доходы и расходы, а потом находят сальдо — разницу между ними. Сделаем то же самое.
Доходы: 525 с первой продажи и столько же со второй. Получается 525 + 525 = 1050 тысяч.
Расходы: 450 за первую машину и 550 за вторую. Получается 450 + 550 = 1000 тысяч.
Сальдо: доходы минус расходы. Это 1050 − 1000 = 50 тысяч.
Опять дважды два.
На картинке один из вирусных примеров, споры об ответе в интернете идут давно, вот и я решил написать опус по данной теме, тем более этот пример мне задавала учитель математики в 5-м классе в далеком 1989 году. Варианта решения данного примера предлагается 2, однако я предложу 4 варианта.
Чтобы решить какую то задачу необходимо знать её условия, все ли условия данной задачи мы знаем? Со сложением всё понятно, с умножением тоже, поскольку знак умножения можно не писать между буквенными значениями и перед скобкой. А что за знак ÷ ? Это обелюс. Чтобы решить задачу необходимо определиться что он обозначает. Многие скажут что это деление. Тогда уточняющий вопрос: какое это деление?
Дело в том, что в России и СССР знак обелюса не использовался в качестве знака деления, в СССР этот знак ÷ использовался для обозначения интервала в инженерии. Таким образом в условии задачи мы должны уточнить в какой области решается данная задача, в математике или инженерии. Если задачу решать в инженерии с учетом значения знака ÷ — обозначение интервала, то задача имеет следующее значение: интервал от 6 до 2 умноженный на (1+2), правильный ответ в этом случае мы получим: интервал от 18 до 6.
Если мы обратимся к истории использования деления то увидим, что в древности для деления использовалась горизонтальная черта, то есть наше выражение в древности при Героне Александрийском будет выглядеть следующим образом:
результат этого действия будет равен единице. Таким образом мы выяснили, что если одно из условий этого примера будет решить его во времена Герона Александрийского то правильный ответ будет равен 1.
Но не обязательно так далеко заглядывать с прошлое, в своей книге Шустеф М. Ф. Методика преподавания алгебры. Курс лекций. Минск, 1967 г. на странице 43 указывает, что в арифметике и алгебре используется разные подходы в порядке действий, Шустеф пишет: «В алгебре тот же порядок действий, что и в арифметике, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например, a : b ⋅ c = a : (b ⋅ c)» и примером делает вывод о том, что умножение имеет приоритет в вычислении перед делением. Тем не менее Алгебра это раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики. Как так получилось, что в арифметику расширили так, что порядок действий изменился? Ясно одно, в результате стандартизации математики в современное время этот пример не должен дать разногласия и на сегодняшний день умножение не имеет приоритет над делением.
Таким образом этот пример если решать в 1967 году то важно будет то, как мы его решаем, по правилам арифметики (ответ будет 9) или по правилам алгебры (ответ будет 1). На сегодня разницы в решении по правилам арифметики и алгебры нет
Что говорит стандарт (ГОСТ Р 54521-2011 и ISO80000-2)? Для деления используются следующие символы: или деление a на b
. Для деления применяют также знак (:). Не следует использовать знак ÷
Теперь нам осталось определиться, мы использовали знак ÷ вместо знака в этом отношении или этом и как произвели замену в случае использования горизонтальной черты, так:
или так:
если первый случай, то ответ 9, если второй то ответ 1, если знак ÷ считаем аналогичный этому / то ответ 9
Если преобразовать в соответствии со стандартом деление в умножение то получим
в которой порядок действий не вызывает сомнения.
Итого получается три варианта решения этой задачи в зависимости от времени, страны и других дополнительных данных. Какой же четвертый вариант решения упомянутый мною в начале статьи? Четвертый вариант ответа буде 0 (ноль). Этот вариант будет в случае использования в Дании и Норвегии и некоторых других странах где знак ÷ используется как символ вычитания, таким образом получается пример 6-2(1+3) = 0.
В современной математике (арифметике и алгебре) порядок действий умножения не имеет приоритета над делением, и при преобразовании по правилам алгебры наше выражение будет иметь вид:
И легко решаться.
Опубликовано в рубрике математика
Рекрутер и бесконечный офис
В одной крупной компании появился безумный рекрутер, который нанимал на работу только джуниоров. У него был хитрый план — заполнить ими весь офис и получить за это премию от начальства. Чтобы это сделать, он каждый день нанимал столько же людей, сколько уже работает в офисе. Грубо говоря, удваивал число джуниоров.
Когда он только начинал, в старом офисе работал только один джуниор, но 30 дней спустя все рабочие места в офисе были полностью заняты напуганными, ничего не понимающими джуниорами.
В новом, точно таком же по размеру офисе с первого дня работает в 2 раза больше людей, чем на старте в старом — целых 2 джуниора вместо одного. Сколько времени уйдёт у безумного рекрутера на то, чтобы заполнить новый офис и получить свою квартальную премию?
Казалось бы, что если на старте в 2 раза больше людей, то и новый офис заполнится быстрее в 2 раза — за 15 дней вместо 30, но это не так.
Смысл в том, что, по условию задачи, рекрутер удваивает число людей каждый день. Это значит, что в новом офисе это удвоение произошло фактически на день раньше, чем в старом, а значит, и джуниоры его полностью займут только на день раньше — за 29 дней вместо 30.
Если вы любите точные математические решения вместо рассуждений — вот решение. Сначала посчитаем, сколько людей всего вмещает каждый офис. Для этого запишем каждые удвоения начиная с одного джуниора:
день 1: 1 джуниор
день 2: 2 джуниора
день 3: 4 джуниора
день 4: 8 джуниоров . . .
Если вывести общую формулу, получим:
день 1: 2 в нулевой степени джуниоров
день 2: 2¹ джуниоров
день 3: 2² джуниоров
день 4: 2³ джуниоров
. . .
день 30: 2 в 29-й степени джуниоров
Получается, что наш офис вмещает 2 в 29-й степени джуниоров. Если удвоение происходит каждый день и на старте у нас 2 джуниора, то для нового офиса получим такое уравнение, где х — количество дней:
2 в 29-й степени = 2 в степени х
Очевидно, что х = 29, а, значит, на заполнение всего нового офиса понадобится 29 дней, как мы и говорили в начале.
Программисты и часы
— Доброе утро. Который сейчас час?
— Сложи 1/4 времени, прошедшего с полуночи до сейчас, с 1/2 от сейчас до полуночи.
— Спасибо, я понял.
— Не сомневался.
Вопрос: который час?
На самом деле это очень простая задача, если помнить, что в сутках 24 часа.
Пусть от полуночи до сейчас прошло Х времени. Тогда от сейчас до полуночи осталось 24 – Х времени.
С другой стороны, если мы сложим четверть времени от полуночи до сейчас и половину времени от сейчас до полуночи, то как раз получим Х — время, которое сейчас:
(¼ × Х) + (½ × (24 − Х)) = Х
Раскрываем скобки:
Х/4 + 12 − Х/2 = Х
Перенесём все Х в одну сторону, а 12 — в другую:
Х − Х/4 + Х/2 = 12
Х + Х/4 = 12
5Х/4 = 12
5Х = 48
Х = 9,6
Получается, что с полуночи прошло 9,6 часа, или 9 часов 36 минут.
Ответ: на часах 9:36.
Порядок выполнения действий, правила, примеры
Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий
Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Полторы белки
Полторы белки за полторы минуты съедают полтора ореха. Сколько орехов съедят 9 белок за 9 минут?
Первое, что хочется сразу ответить — 9 орехов. Но это было бы слишком просто.
Самое безумное в этой задаче — полторы белки. Давайте от них избавимся и будем дальше работать уже с целыми животными.
Дальше в решении будем исходить из того, что белки всё едят одновременно друг с другом, независимо от их количества. В обычной жизни так и происходит, и мы тоже будем придерживаться того же.
Узнаем, на что способна одна белка за полторы минуты:
1,5 белки за 1,5 минуты съедают 1,5 ореха → 1 белка за те же 1,5 минуты съест 1 орех.
Теперь выясним, сколько орехов она съест за 9 минут. Для этого нам нужно полторы минуты умножить на 6, а значит и количество съеденного тоже нужно умножить на 6:
1 белка за (1,5 * 6) минут съест (1 * 6) орехов
↓
1 белка за 9 минут съест 6 орехов.
Осталось запустить 9 белок одновременно и посчитать, сколько орехов они осилят за те же 9 минут:
(1 * 9) белок за 9 минут съедят (6 * 9) орехов
↓
9 белок за 9 минут съедят 54 ореха!
Почему? Потому что математика!
Порядок выполнения действий
В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.
1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
Например,
В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:
Полностью пример записываем так:
Например,
В числовом выражении 3 арифметических действия: деление, умножение и деление.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:
Полностью пример записываем так:
15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2
2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.
Полностью пример записываем так:
3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.
Например,

В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.

Полностью пример записываем так:
Например,

В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.

Полностью пример записываем так:
42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Пример.
Выполните указанные действия 5+(7−2·3)·(6−4):2.
Решение.
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3. В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1. Переходим ко второму выражению в скобках 6−4. Здесь лишь одно действие – вычитание, выполняем его 6−4=2.
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2. В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2.
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6.
Ответ:
5+(7−2·3)·(6−4):2=6.
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Пример.
Выполните действия в выражении 4+(3+1+4·(2+3)).
Решение.
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3). Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5. Подставив найденное значение, получаем 3+1+4·5. В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24. Исходное значение, после подстановки этого значения, принимает вид 4+24, и остается лишь закончить выполнение действий: 4+24=28.
Ответ:
4+(3+1+4·(2+3))=28.
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1. Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1, то после этого исходное выражение примет вид (4+(4+1)−1)−1. Опять выполняем действие во внутренних скобках, так как 4+1=5, то приходим к следующему выражению (4+5−1)−1. Опять выполняем действия в скобках: 4+5−1=8, при этом приходим к разности 8−1, которая равна 7.
Математические примеры
Добро пожаловать на сайт
MathExample.com
Данный образовательный ресурс предназначен для приобретения вами навыков практической математики , а также для развития математических способностей у вас и ваших детей.
” Числа являются интеллектуальными свидетелями, которые принадлежат только человечеству ”
~Оноре де Бальзак
Веб-сайт Цели:
- Расширение знаний по математике
- получение практического опыта решения математических задач
- повышение скорости и качества логического и математического мышления
- развитие памяти, внимательности и концентрации
С помощью этого ресурса вы можете:
- получить базовые знания о сложении, вычитании, умножении и делении
- выучить таблицу умножения с помощью практических упражнений
- выучить операции с целыми, десятичными и дробными числами
- освоить методы решения уравнений
- получить практическое правописание
На сайте предусмотрены следующие возможности:
Возможность мыслить рационально нужно развивать и укреплять, с нами это сделать проще!
10+
Создайте листы математических примеров для деления методом столбца . Числа примера целые числа . Ответы всегда положительные и целые . Всего 1 вариант и 5 уровней сложности.
Числа примера целые числа . Ответы всегда положительные и целые . Всего 1 вариант и 5 уровней сложности.
Делитель
Создает примеры с делением операции целых чисел на столбец метод
1 вариант 5 уровней
вариант: 1 уровень: легкий
12+
Создает рабочие листы с английскими инфинитивами , где некоторые слова отсутствуют. Пропущенные глаголы необходимо дополнить. Всего 3 варианта и 3 уровня сложности.
Инфинитив
Создает рабочие листы с английскими инфинитивами там, где пропущены некоторые слова, необходимо заполнить пропущенные глаголы
3 варианта 3 уровня
Задача про бармена и гурмана
У бармена эксклюзивного лофт-хипста-бара на улице Рубинштейна есть только два одинаковых стакана по 150 мл. Один стакан — полный, и в нём простая вода, а в другом 40-градусная водка, и он наполовину пуст. Утро-с.
В бар зашёл посетитель и попросил сделать ему 15-градусный раствор спирта. Находчивый бармен не растерялся и смог приготовить его, используя только эти два стакана. Как он это сделал и какой объём получился в итоге?
Вряд ли эта задача когда-нибудь попадётся на собеседовании в ИТ-компанию, но она может пригодиться в реальной жизни — например, завтра.
Это вариант классической задачи на переливания, только надо считать ещё крепость раствора и его объём.
Берём полупустой стакан с водкой и доливаем в него воды до полного. Получаем целый стакан 20-градусного спирта ((40 + 0) / 2 = 20). Во втором стакане осталась половина чистой воды, она нам сейчас пригодится.
В стакан с оставшейся водой наливаем наш раствор спирта — снова до краёв. В нём теперь 10 градусов ((20 + 0) / 2 = 10). В другом осталось полстакана 20-градусного спирта.
Финальным этапом бармен берёт и разбавляет эти полстакана 10-градусным раствором из полного стакана так, чтобы жидкость снова дошла до края. В итоге получается 15-градусный раствор ((20 + 10) / 2 = 15) объёмом в 150 мл!
Таракан на стене
В ваш подъезд двумя этажами ниже въехали новые жильцы, которые привезли с собой тараканов, но не привезли еды. Насекомые в поисках еды стали ползти вверх по вентиляционной шахте и скоро доберутся до вашей квартиры. Но карабкаться вверх им неудобно: за час они поднимаются на 1 м, но сразу после этого теряют равновесие и скатываются на ⅔ м вниз.
Вопрос: сколько часов у вас есть на покупку ловушек для тараканов, если расстояние от вас до соседей по вентиляционной шахте — 7 м?
За один полный час таракан проползает ⅓ м: поднимается на метр и опускается на ⅔:
1 — ⅔ = ⅓ м — проползает таракан за час.
С другой стороны, последний метр таракан проползёт тоже за 1 час: он доберётся до верха за 60 минут, но скатываться вниз ему уже не надо, потому что он достиг ровной поверхности. Значит, нужно узнать, сколько времени ему понадобится на оставшиеся 6 м:
7 м до вас — 1 м, который он проползёт за один заход = 6 м, которые таракан будет медленно ползти и скатываться.
Чтобы узнать оставшееся время, разделим расстояние на скорость:
6 м / ⅓ м в час = 18 часов.
Получается, что таракан проползёт 6 м за 18 часов, а оставшийся метр преодолеет за час, потому что скатываться уже не придётся. Получаем общее время:
18 + 1 = 19 часов.
Значит, у вас есть 19 часов на то, чтобы купить ловушки и гель от тараканов. Логика!
Что не так с отчётом?
Один требовательный HR-директор дал задание менеджеру: провести опрос среди веб-программистов и выяснить, на каком языке они пишут чаще всего — на JavaScript или на PHP. Через неделю менеджер принёс такой отчёт:
- количество опрошенных — 300;
- умеет писать на JavaScript — 234;
- умеет писать на PHP — 213;
- умеют писать на обоих языках — 144;
- вообще не пишут код — 0.
HR-директор посмотрел на отчёт и сказал менеджеру «У тебя ошибка в отчёте. Данные фальсифицированы. Ты уволен в связи с утратой доверия». За какую ошибку уволили менеджера?
Чтобы найти ошибку, давайте проверим цифры из отчёта и сравним их с исходными. Для начала выясним, кто умеет писать ТОЛЬКО на JavaScript. Чтобы это сделать, возьмём тех, кто умеет на нём писать, и вычтем оттуда тех, кто пишет на обоих языках:
234 − 144 = 90 (чистых JavaScript-программистов)
Точно так же посчитаем тех, кто пишет ТОЛЬКО на PHP: возьмём общее количество PHP-программистов и вычтем из них тех, кто умеет писать на обоих языках.
213 − 144 = 69 (чистых PHP-программистов)
А теперь сложим три группы: тех, кто пишет только на JavaScript (90 человек), кто пишет только на PHP (69 человек) и тех, кто пишет на двух языках сразу (144 человека).
90 + 69 + 144 = 303
Получилось 303 человека, а в опросе заявлено 300.
Понятно, что расхождение в 3 человека не влияет на общую статистику, но для требовательного HR-директора этого было достаточно.
Простой пример по математике озадачил Тайку Вайтити. Как решить задачу для младшей школы со скобками
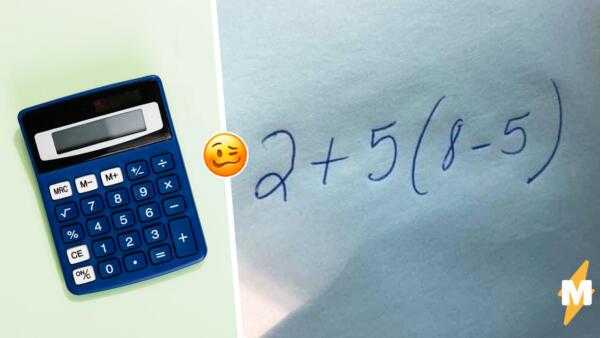
Простая задача по математике на порядок действий разделила пользователей англоязычного твиттера. Любопытные комментаторы пытаются найти правильный ответ примера для младших классов, используя разные, порой несуществующие математические правила. В споре поучаствовал и актёр Тайка Вайтити, но не попал в «список отличников».
Пример со скобками 28 ноября опубликовал пользователь твиттера с ником MIR (@1RealMir) — комментатор запостил фотографию задания и предложил своим подписчикам поделиться полученными ответами. Задача включала в себя вычитание в скобках и сложение за скобками — автор использовал простые числа, поэтому основной трудностью примера был порядок действий.
Какой ответ вы получили?

Твит развирусился, став для части комментаторов настоящей головоломкой. Одним из самых популярных ответов оказалось число 21 — те, кто в ходе решения получил такую цифру, поделились порядком действий. Так, блогерка Tara Dublin (Taylor’s Version) (@taradublinrocks) расписала этапы решения задачки по очереди — сначала девушка сложила цифры за скобками, затем выполнила вычитание в скобках и в конце умножила числа друг на друга.
Вторым популярным ответом стало число 17 — его получила другая половина комментаторов, тоже поделившаяся ходом решения. Как оказалось, ответившие 17 использовали иной порядок действий — после вычитания в скобках фанаты арифметики выполнили умножение и только потом — сложение.
На пост обратил внимание даже новозеландский актёр и кинорежиссёр Тайка Вайтити. В шуточном твите он предположил, что правильный ответ — 3
Что за чертовщина — всё это не имеет смысла. Там стоит число 7, а рядом в скобках 3. Можно прочитать, как «7, но на самом деле это 3», так что верное решение — 3.
На самом деле решение задачи кроется в школьном правиле из начальных классов, порядке действий, которое гласит — вначале выполняются действия в скобках, затем приоритет достаётся умножению и делению, а в конце решаются сложение и вычитание. Применяя математические правила, пример решается простым образом — первым выполняется вычитание в скобках, затем умножение, и после последнего действия, сложения, получаем правильный ответ — 17.
Впрочем, споры вокруг задания продолжаются — пользователи Сети, получившие разные ответы, настаивают на своей правоте.
Ранее Medialeaks рассказал, как простая задача на логику вывела из строя трёх инженеров. Молодые специалисты три минуты пытались понять, как из двух цифр 100 получить двести, используя одну чёрточку.
О том, зачем пользователи Сети ищут слово «цвет» в «Яндексе», читайте в материале Medialeaks. Участники флешмоба таким образом гадают, как на палитре выглядит их настроение.






























