Подгонка чисел
Можно попробовать привести арифметическое вычисление к более удобному виду. Например, произведение чисел 35 и 49 можно себе представить таким образом: 35 * 49 = (35 * 100) / 2 — 35 = 1715
Этот способ может оказаться более эффективным, чем предыдущий, но он не универсальный, и подходит не ко всем случаям. Не всегда можно найти подходящий алгоритм для упрощения задачи.
На эту тему вспомнился анекдот про то, как математик проплывал по реке мимо фермы, и заявил собеседникам, что ему удалось быстро подсчитать количество овец в загоне, 1358 овец. Когда его спросили, как ему это удалось, он сказал, что все просто — нужно подсчитать количество ног, и разделить на 4.
NumberNut.
Арифметика
Мы немного схитрили, введя какое-то двух- и трехзначное умножение в нашу переносную секцию. Однако мы работали с простыми цифрами. Правила просты, если вы умножаете двузначное число на однозначное. Умножьте единицы на , а затем умножьте на десятки.
Пример: 32 x 3 = ? Умножить единицы: 3 x 2 = 6 Умножить десятки: 3 x 3 = 9 32 x 3 = 96
В этом примере не было переноски/перегруппировки. Если у вас есть перенос, вам нужно будет выполнить схему «Умножить — Перенести — Умножить — Добавить».
Пример: 96 x 8 = ? УМНОЖИТЬ ЕДИНИЦЫ: 6 x 8 = 48 НАПИСАТЬ И НОСИТЬ: Напишите «8» и перенесите «4» УМНОЖИТЕ ДЕСЯТКИ: 8 x 9 = 72 ДОБАВИТЬ: Добавьте переносимую сумму.
72 + 4 = 76 ЗАПИСАТЬ: Запишите “76” Ответ: 96 x 8 = 768
Итак, что произойдет, если у вас есть два двузначных числа для ваших делителей ? Хотя это займет немного больше времени, решить проблему несложно. Вам просто нужно решить две задачи на умножение, а затем сложить ответы. Какие? Как это могло быть так просто? Давай посмотрим.
Пример: 96 x 28 = ? Часть 1: Умножьте 8 x 96. Ответ: Из приведенного выше примера мы знаем, что ответ равен 768.
Часть 2: Умножьте 2 x 96. (1) 6 x 2 = 12 (2) Напишите «2» и перенесите «1» (3) 2 x 9 = 18 (4) Доп. 18 + 1 = 19 (5) Напишите «19» Ответ: 96 х 2 = 192
Часть 3: Добавьте два ответа. Как вы думаете, теперь можно просто сложить два значения? Нет! Есть одна хитрость. Когда вы умножаете вторую часть, добавьте к этому ответу «0», потому что вы умножаете значение из столбца десятков (2).
Если это из десятков, добавьте ноль. Если это из сотен, вы должны добавить два нуля.
768 + 1920 = 2688 (видите, как мы добавили «0» к значению «192»?)
Запишем в вертикальном (вверх-вниз) формате. Вам будет проще увидеть настройку.
| 96 x 28 768 + 192 2668 |
Может быть трудно понять, когда эта идея выражена словами, но сама концепция проста. Если ваш второй множитель (или нижний) состоит из двух цифр, вы решаете две задачи на умножение. В следующем разделе вы быстро увидите, что если ваш второй множитель состоит из трех цифр, вы решите три задачи на умножение.
Вторая идея, которую следует знать, заключается в том, что перед добавлением ответов необходимо добавить несколько нулей. При умножении первого значения не добавляйте нули. Когда вы умножаете значение десятков, добавляйте один ноль в конце ответа.
Добавьте два нуля, если есть значение сотен, и три нуля для значения из разряда тысяч. Вы видите шаблон с нулями? Посмотрите, как быстро числа могут стать действительно большими, когда вы их умножаете?
Пример:
| 352 x 231 352 1056 + 704 00 81 312 |
Извините за использование таких больших чисел. Нам нужно показать вам образец. Все умножение было очень простым. Самая сложная задача на умножение, которую мы решали, была 5×3. Когда у вас большие проблемы, просто наберитесь терпения и выполните все шаги.
► СЛЕДУЮЩАЯ СТРАНИЦА ПО АРИФМЕТИКЕ ► ВЕРНУТЬСЯ НА НАЧАЛО СТРАНИЦЫ
► Или выполните поиск на сайтах…
- Обзор
- Операции
- Дополнение
- Вычитание
- Умножение
- от 1 до 10
- Переноска
- Двухзначные номера
- Трехзначные номера
- Несколько значений
- Целые числа
- Отдел
- Мероприятия
Википедия: https://en.
wikipedia.org/wiki/arithmetic Encyclopædia Britannica: Http:/wwwwhwwhwwhwwhwwhwwnica. com: http://www.encyclopedia.com/topic/arithmetic.aspx
Умножение на двузначные и трёхзначные числа / Умножение / Числа больше 1000 / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Числа больше 1000
- Умножение
- Умножение на двузначные и трёхзначные числа
Письменный приём умножения трёхзначных чисел
Общий алгоритм:
1.
Пишу единицы под единицами, десятки под десятками, сотни под сотнями.
2. Умножу первый множитель на число единиц.
3. Умножу первый множитель на число десятков.
4. Умножу первый множитель на число сотен (если есть).
5. Читаю ответ, начиная со старшего разряда.
Умножение на двузначное число:
Пишу: 983 • 16.
Умножу первый множитель на число единиц:
983 • 6 = 5798.
Получу первое неполное произведение: 5798.
Умножу первый множитель на число десятков:
983 • 1 = 983.
Получу второе неполное произведение: 983 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: 15628. Это произведение чисел 983 и 16.
Умножение на трёхзначное число:
Пишу: 518 • 204.
Умножу первый множитель на число единиц:
518 • 4 = 2072.
Получу первое неполное произведение: 2072.
В десятках второго множителя – ноль, поэтому пропускаем этап умножения на десятки.
Умножу первый множитель на число сотен:
518 • 2 = 1036.
Получу второе неполное произведение: 1036 сот.
Начну подписывать второе неполное произведение под сотнями.
Сложу неполные произведения.
Читаю ответ: 105672. Это произведение чисел 518 и 204.
Умножение на трёхзначное круглое число:
Пишу: 766 • 530.
Ноль смещаем вправо и не учитываем его в умножении.
Умножу первый множитель на число единиц:
766 • 3 = 2298.
Получу первое неполное произведение: 2298.
Умножу первый множитель на число десятков:
766 • 5 = 3830.
Получу второе неполное произведение: 3830 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения. Допишу к ответу ноль из второго множителя.
Читаю ответ: 405980. Это произведение чисел 766 и 530.
Советуем посмотреть:
Умножение на однозначные числа
Классы и разряды.
Состав числа. Сравнение чисел.
Сложение
Вычитание
Умножение
Деление
Числа больше 1000
Раскладка по разрядам
Является самым простым приемом быстрого умножения двухзначных чисел. Оба множителя нужно разбить на десятки и единицы, а затем все эти новые числа перемножить друг на друга.
Данный способ требует умения удерживать в памяти одновременно до четырех чисел, и делать с этими числами вычисления.
К примеру, нужно перемножить числа 38 и 56. Делаем это следующим образом:
38 * 56 = (30 + 8 ) * (50 + 6) = 30 * 50 + 8 * 50 + 30 * 6 + 8 * 6 = 1500 + 400 + 180 + 48 = 2128 Еще проще будет делать устное умножение двухзначных чисел в три действия. Сначала нужно перемножить десятки, затем прибавить два произведения единиц на десятки, и затем прибавить произведение единиц на единицы. Выглядит это так: 38 * 56 = (30 + 8 ) * (50 + 6) = 30 * 50 + (8 * 50 + 30 * 6) + 8 * 6 = 1500 + 580 + 48 = 2128 Для того, чтобы успешно пользоваться этим способом, нужно хорошо знать таблицу умножения, уметь быстро складывать двухзначные и трехзначные числа, и переключаться между математическими действиями, не забывая промежуточные результаты. Последнее умение достигается с помощью тренировки зрительной памяти и визуализации.
Данный способ не самый быстрый и эффективный, потому стоит изучить еще и другие способы устного умножения.
Русский способ умножения
Способ этот, был употребителен в обиходе русских крестьян и унаследован ими от глубокой древности. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа, таблица умножения в этом деле без надобности
Деление пополам продолжают до тех пор, пока в частном не получится 1, при этом параллельно удваивают другое число. Последнее удвоенное число и даёт искомый результат (рисунок 1). Нетрудно понять, на чём этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение.
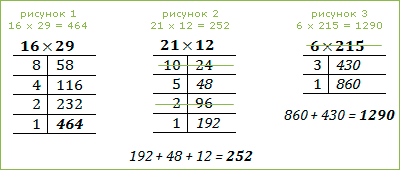
Однако как поступить, если при этом приходится делить пополам нечётное число? В этом случае от нечётного числа откидываем единицу и делим остаток пополам, при этом к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечётных чисел левого столбца – сумма и будет искомым произведением (рисунки: 2, 3).
Иными словами все строки с чётными левыми числами зачёркиваем; оставляем, а затем суммируем не зачёркнутые числа правого столбца.
Для рисунка 2: 192 + 48 + 12 = 252
Правильность приёма станет ясна, если принять во внимание, что:
5 × 48 = (4 + 1) × 48 = 4 × 48 + 48
21 × 12 = (20 + 1) × 12 = 20 × 12 + 12
Ясно, что числа 48, 12, утрачиваемые при делении нечётного числа пополам, необходимо прибавить к результату последнего умножения, чтобы получить произведение.Русский способ умножения и элегантен и экстравагантен одновременно
§ Логическая задачка о Змее Горыныче и прославленных русских богатырях на зелёной страничке «Кто из богатырей победил Змея Горыныча?»
решение логических задач средствами алгебры логикиДля тех, кто любит учиться! Для тех, кому в радость гимнастика для ума
§ Решение логических задач табличным способом
Продолжаем разговор
Суть японской системы умножения
Давайте попытаемся разобрать это на примере:
Чтобы умножить 23 × 45, нам нужно изобразить число 23, поэтому нарисуем круги: два «двойных» для десятков и два «тройных» для единиц.
Почему мы рисуем именно два круга каждого вида?
Причина заключается в том, что число 23 мы умножаем на двухзначный множитель 45. Здесь мы будем изображать каждый из множителей сверху вниз и слева направо, также, как и в китайском способе.
Далее переходим к числу 45, которое нам нужно будет тоже изобразить.
Для этого, начиная с верхнего левого угла и двигаясь по столбикам, нам необходимо разделить круги на четыре и на пять частей (45) так же, как показано на рисунке.
При этом сектора кругов не должны быть равными по размеру. Их можно примерно разделить и на глаз, главное здесь – количество самих частей.
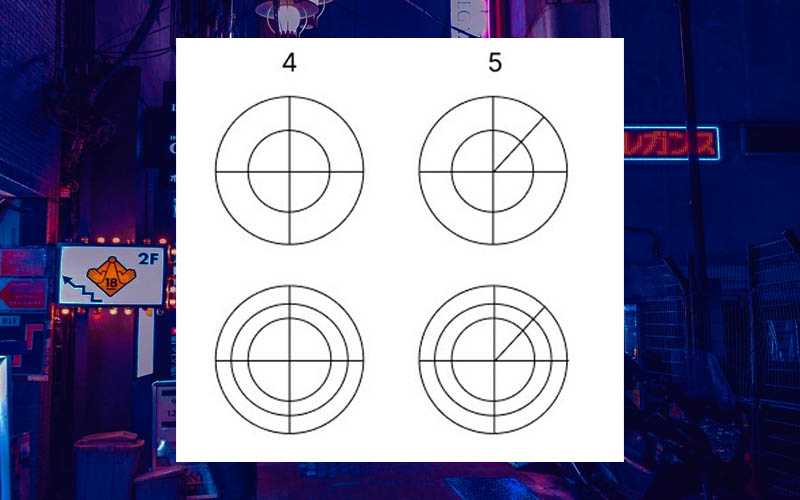
После этого нам нужно подсчитать количество секторов, образовавшихся в результате деления этих колец. Для большего удобства мы можем ставить точку в каждом секторе ручкой.
Далее эти круги снова делим на группы, точно также, как в китайском способе: нижний правый угол – это единицы, диагональ – идут десятки, и верхний левый угол – это сотни.
В итоге в результате такого умножения получается 15 единиц, 22 десятка и 8 сотен, то есть, нам снова нужно будет применить правило перехода через десяток.
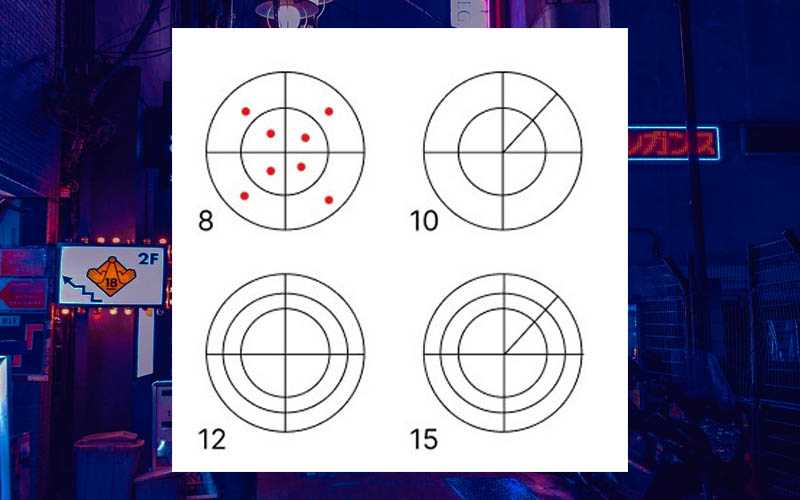
Продолжаем начинать с единиц.
От 15 будем оставлять пятерку и «перебросим» единицу в следующий разряд.
Далее в разряде десятков получилось 22 + 1 = 23 десятка, мы оставим тройку, а двойку снова «перебросим» в старший разряд.
У нас стало сотен 8 + 2 = 10, другими словами, десять сотен – это тысяча.
Формируем ответ:
Тысяча + три десятка + пять единиц и в результате имеем 23 × 45 = 1035.
Японский способ очень удобен, в первую очередь, своей наглядностью. Поскольку все изображено на бумаге, значит не требуется в голове производить одновременно множество арифметических действий. Такой способ отлично подходит для умножения даже тем, кто не знает таблицу.
Тем не менее данный метод имеет некоторые минусы.
Например, при этом умножении не очень удобно вычислять произведения четырехзначных, а также более крупных чисел, потому что запись становится очень громоздкой и в ней можно легко запутаться.
Поэтому, когда речь идет о больших числах, лучше находить произведение таких больших чисел привычным нам всем «столбиком».
Когда требуется умножить разные числа, например двузначные на трехзначные, тогда проще всего воспользоваться именно японским методом с кругами, в отличие, например, от китайского способа с линиями. Тогда таблица из кругов будет иметь не квадратную форму, а прямоугольную, например, 2 × 3, но суть всех действий останется неизменной.
Китайский и японский счет на пальцах
Кроме классической системы умножения в странах Азии очень даже сейчас популярна дактилономия, то есть вычисления при помощи пальцев. Такой способ практикуют во время обучения малышей и активно применяют на торговле, если под рукой нет калькулятора. Главное, что нужно знать о том, как китайцы считают на пальцах:
- Число определяется тем, какой палец вы показываете, в каком положении, как при этом расположена ладонь и т.д. Также используются комбинации. Например, чтобы показать шестерку, необходимо большой палец и мизинец оставить прямыми, а остальные сжать в кулак.
- Для перемножения больших чисел применяются фаланги пальцев и пространство между ними, чтобы показать цифры от одного до девяти. В качестве указателя используют ногти на больших пальцах.
- Определить разрядность можно по пальцу, например, безымянный демонстрирует сотни, средний – десятки, а указательный – единицы.
- Чтобы показать ноль, достаточно показать на пропуск между пальцами.
В зависимости от провинции в методике и значениях могут быть отличия.
Умножение по японской методике отличается от китайского:
- начинается счет с открытой ладони;
- поджатые пальцы, начиная с большого, показывают числа от 1 до 5, а для демонстрации цифр от 6 до 10 десяти пальцы от мизинца по одному разжимают;
- чтобы показать десятку, достаточно показать собеседнику две раскрытые ладони;
- при общении с европейцами счет начинается с выпрямленного указательного пальца, обозначающего единицу.
Научиться считать и умножать, как в других странах, стоит каждому, ведь это не только прекрасная зарядка для ума, но и веселое времяпровождение!
Визуализация с расстановкой чисел
Очень интересный способ перемножения двухзначных чисел следующий. Нужно последовательно перемножить цифры в числах, чтобы получились сотни, единицы и десятки.
Допустим, Вам нужно умножить 35 на 49.
Сначала перемножаете 3 на 4, получаете 12, затем 5 и 9, получаете 45. Записываете 12 и 5 , с пробелом между ними, а 4 запоминаете.
Получаете: 12 __ 5 (запоминаете 4).
Теперь умножаете 3 на 9, и 5 на 4, и суммируете: 3 * 9 + 5 * 4 = 27 + 20 = 47.
Теперь нужно к 47 прибавить 4, которое мы запомнили. Получаем 51.
Пишем 1 в середине, а 5 прибавляем к 12, получаем 17.
Итого, число, которое мы искали, 1715, оно является ответом:
35 * 49 = 1715
Попробуйте таким же образом перемножить в уме: 18 * 34, 45 * 91, 31 * 52.
Важно разнообразие
Правообладатель иллюстрации
Все способы хороши, главное — чтобы ответ сошелся
Что точно можно утверждать, — так это то, что все эти разные способы дали нам один и тот же результат!
Нам все-таки пришлось кое-что перемножить в процессе, но каждый шаг был проще, чем при умножении традиционным способом, и гораздо более наглядный.
Так почему же мало где в мире в обычных школах учат этим методам вычисления?
Одной из причин может быть упор на обучение «вычислениям в уме» — чтобы развивать умственные способности.
Однако Дэвид Уиз, учитель математики из Канады, работающий в государственных школах в Нью-Йорке, объясняет это иначе.
«Недавно я прочитал, что причина, по которой используется традиционный метод умножения, — это экономия бумаги и чернил. Этот метод не был придуман как самый простой для использования, но как самый экономный с точки зрения ресурсов, поскольку чернила и бумага были в дефиците», — объясняет Уиз.
Правообладатель иллюстрации
Для некоторых методов вычисления только головы недостаточно, нужны еще и фломастеры
Невзирая на это, он полагает, что альтернативные методы умножения очень полезны.
«Я не думаю, что это полезно — сразу учить школьников умножению, заставляя их выучивать таблицу умножения, но не объясняя им при этом, откуда она взялась. Поскольку если они забудут одно число, то как они смогут продвинуться в решении задачи? Метод майя или японский метод необходим, потому что с его помощью вы можете понять общую структуру умножения, а это хорошее начало», — полагает Уиз.
Существует и ряд других способов умножения, например, русский или египетский, они не требуют дополнительных навыков рисования.
Как говорят специалисты, с которыми мы беседовали, все эти методы помогают лучше понять процесс умножения.
«Понятно, что все идет на пользу. Математика в сегодняшнем мире открыта как внутри, так и снаружи классной комнаты», — резюмирует Андреа Васкес, учительница математики из Аргентины.
Исследовательская работа по математике в начальной школе
Краткая аннотация исследовательской работы
Оглавление
«Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным».
Б. Паскаль
Введение
Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики нас в первую очередь учат выполнять действия над числами, то есть считать. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе. Возник вопрос: а есть ли еще какие-нибудь альтернативные способы вычислений? Мне захотелось изучить их более подробно. В поисках ответа на возникшие вопросы было проведено данное исследование.
Цель исследования: выявление нетрадиционных способов умножения для изучения возможности их применения. В соответствии с поставленной целью нами были сформулированные следующие задачи:
— Найти как можно больше необычных способов умножения.
— Научиться их применять.
— Выбрать для себя самые интересные или более легкие, чем те, которые предлагаются в школе, и использовать их при счете.
— Проверить на практике умножения многозначных чисел.
— Провести анкетирование учащихся 4-х классовОбъект исследования:
различные нестандартные алгоритмы умножения многозначных чисел
Предмет исследования: математическое действие «умножение»
Гипотеза: если существуют стандартные способы умножения многозначных чисел, возможно, есть и альтернативные способы.Актуальность
: распространение знаний об альтернативных способах умножения.Практическая значимость
. В ходе работы было решено множество примеров и создан альбом, в который включены примеры с различными алгоритмами умножениями многозначных чисел несколькими альтернативными способами. Это может заинтересовать одноклассников для расширения математического кругозора и послужит началом новых экспериментов.
Глава 1. Альтернативные способы умножения
1.1. Немного истории
1.2. Русский крестьянский способ умножения
1.3. Умножение способом «Маленький замок»
1.4. Умножение чисел методом «ревность» или «решётчатое умножение»
1.5. Китайский способ умножения
1.6. Японский способ умножения
1.7. Таблица Оконешникова
1.8. Умножение столбиком.
2.1. Крестьянский способ
2.2. Маленький замок
2.3. Умножение чисел методом «ревность» или «решётчатое умножение»
2.4. Китайский способ
2.5. Японский способ
Заключение
Список источников информации
Китайское, или японское, умножение
В азиатских странах принято умножать числа не в столбик, а рисуя линии
Для восточных культур важно стремление к созерцанию, и визуализации, поэтому, наверное, они и придумали такой красивый метод, позволяющий перемножать любые числа. Сложен этот способ только на первый взгляд. На самом деле, большая наглядность позволяет использовать этот способ гораздо эффективнее, чем умножение в столбик.
На самом деле, большая наглядность позволяет использовать этот способ гораздо эффективнее, чем умножение в столбик.
Кроме того, знание этого древнего восточного етода повышает Вашу эрудицию. Согласитесь, не каждый может похвастаться тем, что знает древнюю систему умножения, которой китайцы пользовались еще 3000 лет назад.
- pro444.ru
Давайте порисуем!
Как минимум три способа умножения связаны с рисованием пересекающихся линий.
1. Способ индейцев майя, или японский метод
Относительно происхождения этого способа существует несколько версий.
Media playback is unsupported on your device
Трудно умножать в уме? Попробуйте метод майя и японцев
Некоторые говорят, что его придумали индейцы цивилизации майя, населявшие районы Центральной Америки до прибытия туда конкистадоров в XVI веке. Он также известен как японский метод умножения, поскольку учителя в Японии используют именно этот визуальный способ, когда учат младших школьников умножению.
Суть в том, что параллельные и перпендикулярные линии представляют цифры тех чисел, которые нужно перемножить.
Давайте умножим 23 на 41.
Для этого нам надо нарисовать две параллельные линии, представляющие 2, и, немного отступя, еще три линии, представляющие 3.
Затем, перпендикулярно к этим линиям мы нарисуем четыре параллельные линии, представляющие 4 и, чуть отступя, еще одну линию для 1.
Теперь нам надо пересчитать все точки пересечения этих линий. Именно так мы и получаем наш результат — 943, как если бы мы умножали в столбик.
Ну как, неужели трудно?
2. Индийский способ, или итальянское умножение «решеткой» — «джелозия»
Происхождение этого способа умножения тоже не ясно, однако он хорошо известен по всей Азии.
«Алгоритм «джелозия» передавался из Индии в Китай, затем в Аравию, а оттуда в Италию в XIV-XV веках, где он получил название «джелозия», поскольку внешне был похож на венецианские решетчатые ставни», — пишет Марио Роберто Каналес Виллануэва в своей книге, посвященной различным способам умножения.
Image caption
Индийская или итальянская система умножения похожа на венецианские жалюзи
Давайте снова возьмем пример с умножением 23 на 41.
Теперь нам потребуется начертить таблицу из четырех клеток — по клетке на цифру. Подпишем сверху у каждой клетки соответствующую цифру — 2,3,4,1.
Затем надо разделить каждую клетку надвое по диагонали, чтобы получились треугольники.
Теперь мы сначала умножим первые цифры каждого числа, то есть 2 на 4, и запишем в первом треугольнике 0, а во втором 8.
Потом перемножим 3×4 и запишем 1 в первом треугольнике, а 2 во втором.
Проделаем то же самое и с другими двумя цифрами.
Когда все клетки нашей таблицы будут заполнены, мы складываем цифры в такой последовательности, как показано на видео, и записываем получившийся результат.
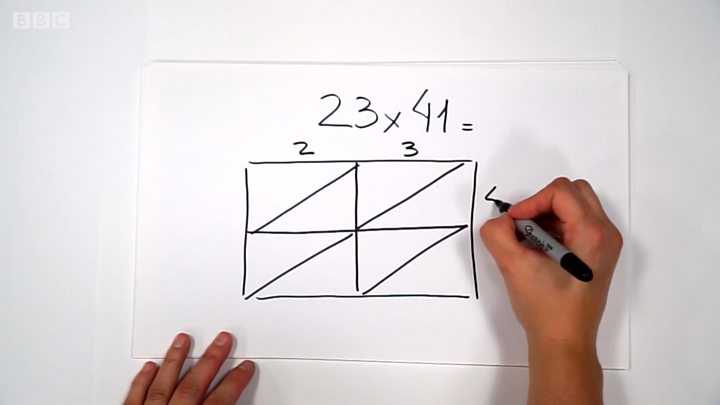Media playback is unsupported on your device
Трудно умножать в уме? Попробуйте индийский метод
Первая цифра у нас будет 0, вторая 9, третья 4, четвертая 3. Таким образом, результат получился: 943.
Как вам показалось, проще этот способ или нет?
Давайте попробуем еще один метод умножения с помощью рисунка.
3. «Массив», или метод таблицы
Как и в предыдущем случае, для этого потребуется нарисовать таблицу.
Возьмем тот же пример: 23 x 41.
Тут нам надо разделить наши числа на десятки и единицы, поэтому 23 мы запишем как 20 в одной колонке, и 3 в другой.
По вертикали мы запишем наверху 40, а внизу 1 .
Затем мы перемножим числа по горизонтали и вертикали.
Media playback is unsupported on your device
Трудно умножать в уме? Нарисуйте таблицу.
Но вместо того чтобы умножать 20 на 40, мы отбросим нули и просто перемножим 2 x 4, получив 8.
То же самое сделаем, умножая 3 на 40. Мы удерживаем в скобках 0 и умножаем 3 на 4 и получаем 12.
Проделаем то же самое с нижним рядом.
Теперь добавим нули: в левой верхней клетке у нас получилось 8, но мы отбросили два нуля — теперь мы их допишем и получится 800.
В правой верхней клетке, когда мы умножали 3 на 4(0), у нас получилось 12; теперь мы допишем ноль и получим 120.
Сделаем так же со всеми прочими удержанными нулями.
И наконец, мы складываем все четыре числа, полученных умножением в таблице.
Результат? 943. Ну как, помогло?
Японский метод умножения в младших классах
Организация: Первомайская СОШ Цивильского района Чувашской Республики
Населенный пункт: Республика Чувашия, д. Вторые Вурманкасы
Цель внеклассного занятия: расширить знания об умножении чисел.
Задачи :
*образовательные: ознакомиться японским методом умножения двузначных чисел, закреплять знания таблицы умножения и деления на однозначное число; продолжать работу по формированию вычислительных навыков;
*развивающие: развивать логическое мышление, умение анализировать и выделять главное, логически строить план решения; развивать самостоятельность, умение преодолевать трудности; развивать навык общения;
*воспитательные: продолжить работу по воспитанию взаимопомощи, культуры общения, способствующей созданию благоприятного психологического климата, внимания, самоконтроля, интереса к предмету, аккуратности.
Структура и ход урока
1. Организационный момент.
Слайд№1
Посмотрите на солнышко, какое оно радостное. А ведь в каждом из нас есть маленькое солнце. Это доброта. Я очень хочу, чтобы урок был для вас действительно добрым и тёплым.
-Ребята, вы хотели бы найти клад? А что это такое?
-Клад – это богатство, деньги, золото.
— Правильно. Но есть на земле гораздо ценнее золота и денег. Их нельзя потратить, с годами их становится всё больше. Это знания. Именно за таким кладом мы сегодня отправимся. Нас ждут трудности и опасности, но мы с ними обязательно справимся. Итак, в путь!
2. Определение задачи и целей урока. Слайд 2.
-Послушайте стих. С. Маршака.
Таблица умножения
Достойна уважения,
Она всегда во всём права:
Чтоб ни случилось в мире,-
А всё же будет дважды два
По-прежнему четыре.
Таблицу каждый должен знать
Обязательно на «5».
— Можете предположить, над чем будем работать сегодня?
-Какие задачи ставим перед собой?
( Проверить свои знания. Посмотреть, как запомнили таблицу.)
3. Запись числа.
-Открыли тетради. Запишите сегодняшнее число.
4.Актуализация знаний.
-Какое сегодня число? (14 ).
-Что можно сказать об этом числе? ( Двузначное, в нём 1 десяток и 4 единицы, чётное. )
-Какие могут быть множители ? (7 и2, 2 и 7).
5. Игра «Делится – не делится».
На доске плакат с числами-произведениями таблицы умножения.
-Ребята, кто хочет быть в роли учителя?
Один ученик выходит к доске и показывает числа. Если это число делится на 4, то дети хлопают.
6. Работа по теме. Слайд 3.
Сегодня мы с вами отправимся в интересную страну.
Если вы правильно решите примеры и расставите ответы в порядке возрастания, то узнаете как она называется.
7 * 3
8 * 6
42: 7
7 * 4
5 * 7
45 : 5
Ответы детей.
21 48 6 28 35 9-
О Я Я Н И П
Слайд 4.
Япония — это уникальное азиатское островное государство, история которого насчитывает тысячелетия. Это особый мир, который превратился в высокоразвитую территорию, сохранив давние традиции. И одна из этих традиций это умножение чисел.
7. Создание проблемной ситуации.
— Ребята, посмотрите на доску. Решите этот пример.12*13 Слайд 5.
— Что вы хотите сказать? Можем мы такой пример решить? Да, мы не учили умножение таких чисел.
А ведь легко и быстро можно решить его. В японских школах дети умножают числа с помощью простого рисунка (кстати, в Китае тоже пользуются этой методикой).
Умножая числа таким способом вовсе не обязательно знать таблицу умножения. Надо всего лишь правильно начертить линии, сосчитать количество пересечений и вывести результат. Просто как всё гениальное.
Давайте проверим 4*2=
Рисуем 4 линии , а поперек еще 2 . Обводим секцию пересечения и считаем точки пересечения. Их 8. Получаем 2х4=8 Значит японский метод работает.
8. Решение примера12*13. Вывешиваю плакат. Слайд 4.
Вот теперь попробуем таким же методом решить наш сложный пример.
1.Рисуем первое число
12 это 1 десяток и 2 единицы
2.Рисуем 2 число
13 это 1 десяток и 3 единицы
3. Начинаем считать пересечения слева — это сотни, потом по диагонали (десятки), а потом справа – единицы. Слева 1 сотня, 5 десятков, 6 единиц. Результат 156
Полный текст статьи см. в приложении.
Приложения:
-
file0.docx.. 29,8 КБ