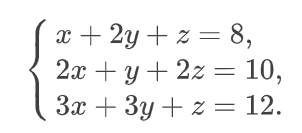14 лучших фильмов про математиков

Пункт 32. Ответы к теме Сложение и вычитание десятичных дробей, страница 75

Задание 361

На пальто израсходовали 3,2 м ткани, а на костюм − 2,63 м. Сколько ткани израсходовали на пальто и костюм вместе? Решите задачу сложением десятичных дробей и путём перехода к сантиметрам.

Решение

Задание 362

Масса автомобиля «Нива» 11,5 ц, а масса автомобиля «Волга» 14,2 ц. На сколько масса «Волги» больше массы «Нивы»? Решите задачу с помощью десятичных дробей и переводом данных в килограммы.

Решение

Задание 363

Выполните сложение:а) 0,769 + 42,389;б) 5,8 + 22,191;в) 95,381 + 3,219;г) 8,9021 + 0,68;д) 2,7 + 1,35 + 0,8;е) 13,75 + 8,2 + 0,115.

Решение

Выполните вычитаниеа) 9,4 − 7,3;б) 16,78 − 5,48;в) 7,79 − 3,79;г) 11,1 − 2,8;д) 88,252 − 4,69;е) 6,6 − 5,99.

Решение

Задание 365

С одного участка собрали 95,37 т зерна, а с другого − на 16,8 т больше. Сколько тонн зерна собрали с двух участков?

Решение

Задание 366

Один тракторист вспахал 13,8 га земли, что оказалось на 4,7 га меньше, чем вспахал второй тракторист. Сколько гектаров земли вспахали оба тракториста вместе?

Решение

От куска провода длиной 30 м отрезали 4,75 м. Сколько метров провода осталось в куске?

Решение

Задание 368

Груз, поднимаемый вертолётом, легче вертолёта на 4,72 т. Какова масса вертолёта вместе с грузом, если масса груза 1,24 т?

Решение

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, которое содержит переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.

А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Квадратные уравнения могут иметь два корня, один корень или не иметь корней.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b2 − 4ac

А вот свойства дискриминанта:

• если D < 0, корней нет;
• если D = 0, есть один корень;
• если D > 0, есть два различных корня.

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Разобраться в теме еще быстрее с помощью опытного преподавателя можно
на курсах по математике в онлайн-школе Skysmart.

3.2. Решение задач на постоянный и переменный ток.

Задача 18 . Сила тока в проводнике меняется со временем по уравнению

i =4 + 2t, где i — в амперах, t — в секундах.

Какое количество электричества протекает через поперечное сечение завремя от t1 = 2 секундам до t2 = 6 секундам?

При какой силе постоянного тока через поперечное сечение проводника­за это же время пройдет такое же количество электричества?

Дано : i =4 + 2t, t1 = 2 с, t2 = 6 с

Найти : q-? Iср-?

Решение:

а) Из определения мгновенного значения силы тока  i =   (1)

выражаем  dq= i·dt         (2)

Интегрируя (2), находим:

q=  (3) 

б) Силу постоянного тока, при котором через сечение провод­ника проходит за то же время такое же количество электричества, что и при данном переменном токе, называют средним значением силы данного перемен­ного тока.

Найдем его:

Iср=

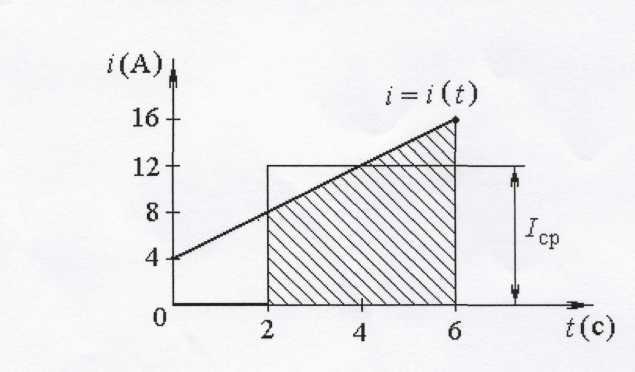
  Рис. 19

На рис. 19 площадь заштрихованной трапеции числено равна q, высота прямоугольника, равновеликого трапеции, равна Iср.

Ответ: Через поперечное сечение протекает количество электричества, равное 48 Кл и среднее значение силы данного перемен­ного тока равно 12 А.

Задача 19.

Найти действующее (эффективное) значение синусоидального переменного тока.

Решение:

Действующим (эффективным) значением силы переменного тока называют силу такого постоянного тока, который в том же сопротивлении за то же время выделяет столько же теплоты, сколько и данный переменный ток. Иными словами, это сила такого постоянного тока, который в смысле теп­лового действия эквивалентен данному переменному току.

Пусть мгновенное значение силы периодического переменного тока  i=i(t). Обозначим Т — период изменения тока. По закону Джоуля — Ленца ко­личество теплоты dQ, выделяемое за время dt в сопротивлении R переменным током i:

  dQ = i2Rdt  (1)

Количество теплоты, выделяемое за один период:

  Q=  (2)

Количество теплоты, выделяемое постоянным током I за то же время: 

  Q = I2RT  (3)

Приравнивая правые части (2) и (3), имеем:

  I2RT =  R,  (4)

Откуда  I =  ,  (5)

т. е. эффективное значение силы переменного тока, по-существу, является его среднеквадратичным значением.

Мгновенное значение силы синусоидального переменного тока:

t= Im· sinщt  (6)

где Im — амплитудное значение тока, щ=  — циклическая частота.

В этом случае

  (7)

Так как:

Подставляя выражение (7) в (5), находим:

I =   (8)

Получается, что  действующее значение синусоидального переменного тока в раз меньше амплитудного.

Аналогично, действующее значение синусоидального напряжения:

U =   (9)

Отметим, что соотношения (8) и (9) справедливы именно для синусои­дального переменного тока. Если ток изменяется с течением времени, каким-то иным образом, эти соотношения перестают быть справедливыми.

Задача 20. Найти среднее значение синусоидального переменного тока

i = Im sinщt а промежуток времени от t1=0 до  t2 = (за половину периода).

Решение:

Из определения мгновенного значения силы тока:

  i=можно выразить dq=i·dt  (1)

Интегрируя (1), выразим заряд q, прошедший через поперечное сечение проводника за промежуток времени от t1 до t2:

q=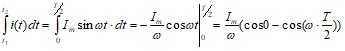  (2)  Учитывая, что  щ =   представим (2) в виде:

  q =   (3)  (3) Находим среднее значение силы тока:

Канал спокойной музыки

  Iср =   (4) 

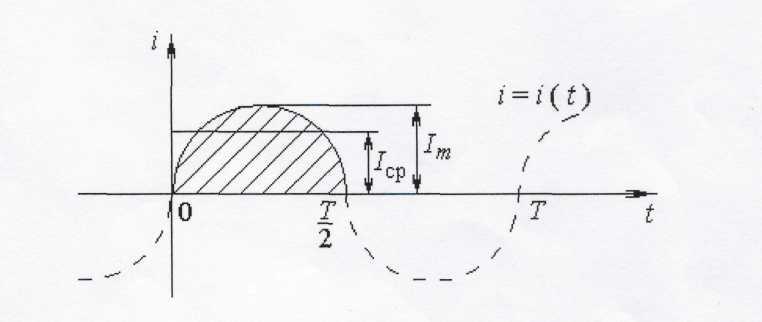
  Рис.20

На рис. 20 площадь заштрихованной фигуры числено, равна q, а высота равновеликого этой фигуре прямоугольника числено, равна Iср.

Определение числовой последовательности

Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.

Последовательности можно задавать разными способами:

1. Словесно — когда правило последовательности объясняется словами:

   «Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23…»

2. Аналитически — когда указана формула ее n-го члена: y_n = f(n).

   Последовательность y_n = C называют постоянной или стационарной.

3. Рекуррентно — когда указывается правило, которое помогает вычислить n-й член последовательности, если известны её предыдущие члены.

   Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: a_n+1 = a_n + a_n-1.

   Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…

   

   

   

   

   

   

   

   

   

   

4. Графически — когда график последовательности состоит из точек с абсциссами
   1, 2, 3, 4…

Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.

Свойства числовых последовательностей:

1. Последовательность {y_n} называют возрастающей, если каждый ее член кроме первого больше предыдущего:

   y₁ < y₂ < y₃ < … < y_n < y_n+1 < …

2. Последовательность {y_n} называют убывающей, если каждый ее член кроме первого меньше предыдущего:

   y₁ > y₂ > y₃ > … > y_n > y_n+1 > …

   Возрастающие и убывающие последовательности называют монотонными последовательностями.

3. Последовательность можно назвать периодической, если существует такое натуральное число T, что начиная с некоторого N, выполняется равенство: y_n = y_n+T. Число T — длина периода.

Запишем числа, которые первые пришли в голову: 7, 19, 0, −1, −2, −11, 0… Сколько бы чисел не написали, всегда можно сказать, какое из них первое, какое — второе и так до последнего. То есть мы можем их пронумеровать.

Пример числовой последовательности выглядит так:

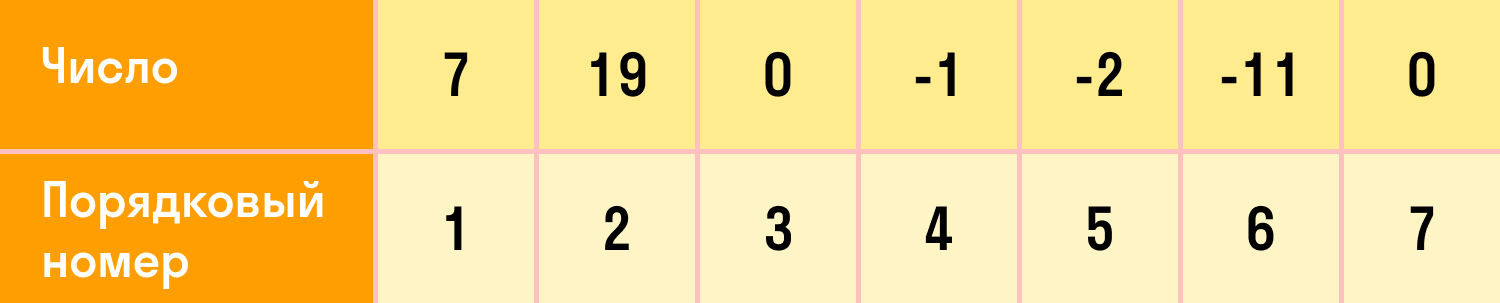
В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.

N-ный член алгебраической последовательности — это число с порядковым номером n.

Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a₁, a₂,…, a₁₀…, a_n.

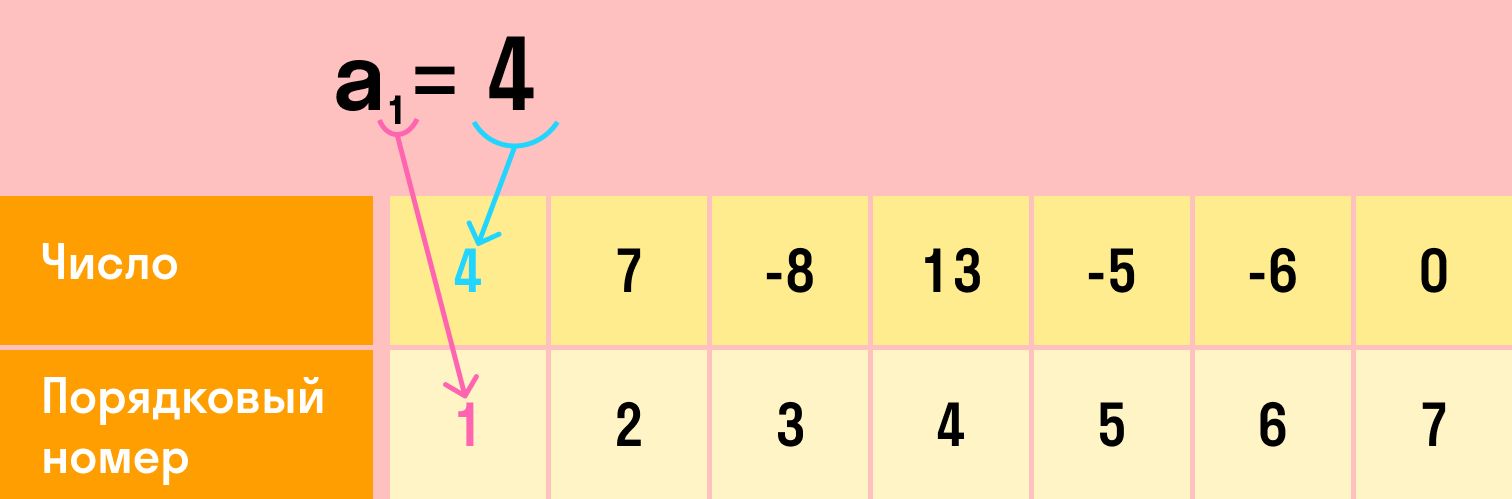
N-ый член последовательности можно задать формулой. Например:

• Формула a_n = 3n − 5 задает последовательность: −2, 1, 4, 7, 10…
• Формула a_n = 1 : (n + 2) задает последовательность: 1/3, 1/4, 1/5, 1/6…

3.1. Простейшие интегралы. Решение задач на нахождение работы и энергии.

Задача 16. Какую работу нужно совершить, чтобы насыпать кучу песка конической формы, радиус основания которой R, а высота h? Плотность песка ρ. Песок поднимают с поверхности земли.

Решение:

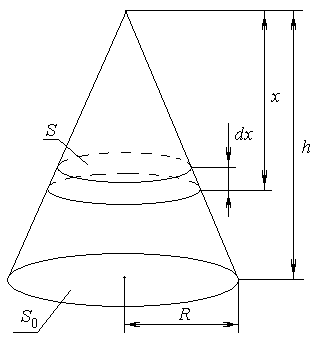
Рис. 17

Мысленно выделим в конусе поперечное сечение на расстоянии х от вершины. Обозначим S – его площадь. При этом , откуда

                                               (1)

Элементарная (т. е. бесконечно малая) работа dA по подъему слоя песка площадью S и толщиной dx, равная приросту потенциальной энергии этого слоя:

                                       (2)

Подставим (1) в (2):

                                       (3)

или

                                       (4)

Интегрируя (4), находим:

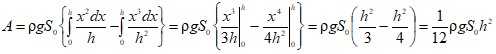       (5)

Так как для прямого кругового конуса , получим

При R = 1,2 м, h = 1 м и ρ = 2⋅102 кг/м3, А ≈ 8⋅103 Дж.

Задача 17. Размеры пирамиды Хеопса приблизительно таковы: высота h = 140 м, сторона основания (квадрата) а = 200 м, плотность материала ρ ≈ 2,5⋅103 кг/м3. Вычислить работу А, затраченную при ее постройке на преодоление силы тяжести.

Решение:

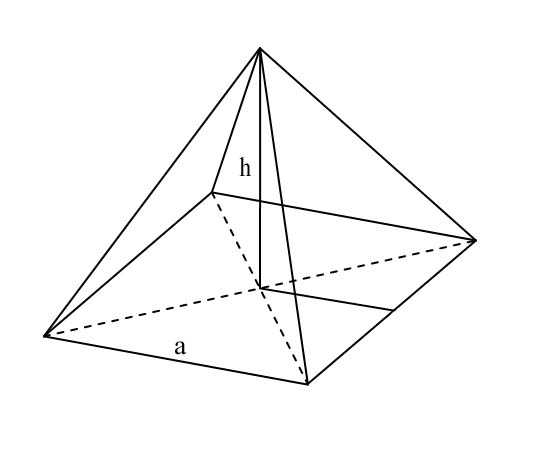
Рис.18

Рассуждения, аналогичные приведенным ранее позволяют вывести формулу

в данной задаче , тогда

Подставляя числовые значения, получим

А ≈ 1,7⋅1012 Дж.

Примечание: задачи такого типа легко решаются, если воспользоваться тем фактом, что центр тяжести пирамиды (или конуса) отстоит от основания на высоты (соответственно, от вершины на высоты).

Западня Ферма

Рейтинг	Кинопоиск — 6.7/ IMDB — 6.6
Жанр	Триллер, детектив
Производство	Испания / 2007
Сборы в мире	$979 921
Режиссёр	Луис Пьедраита, Родриго Сопенья
В ролях	Алехо Саурас, Элена Бальестерос, Льюис Омар, Санти Мильян, Федерико Луппи, Ариадна Каброль, Сан Еламос, Алисия Фернандес, Сеск Корнет, Жуанма Фалькон

Четыре незнакомых друг с другом блестящих математика приглашены таинственным хозяином Ферма под предлогом решения величайшей числовой загадки всех времён. Получив псевдонимы – Галуа, Гильберт, Оливия и Паскаль, они изо всех сил пытаются решить головоломки и определить – почему они здесь?

Ставки становятся выше, поскольку стены запертой комнаты буквально начинают сжиматься вокруг них. В гонке со временем получится ли у них узнать, что их всех связывает и почему кто-то хочет их убить?

«Эпизод с Унаги» (6 сезон, 17 серия)

Несмотря на то, что Росс был профессором, он никогда не боялся проявлять творческий подход и играть по своим собственным правилам. В 6 сезоне он почувствовал необходимость научить своих друзей искусству унаги, которое, как он утверждал, означало гиперосведомленность об окружающей среде.

У Рэйчел этого не было, и она продолжала настаивать на том, что унаги — это разновидность суши, что побуждало Росса несколько раз пытаться скрытно атаковать ее. Рэйчел и Фиби в конце концов подшучивали над ним и пугали его собственными унаги. Это была веселая сюжетная линия, подчеркнувшая причуды характера Росса, особенно его неспособность оставить все как есть.

Решение системы линейных уравнений методом Гаусса

Этот метод позволяет достаточно легко находить решения систем линейных уравнений, в которых более двух уравнений и неизвестных. По сути, этот метод является обобщением метода подстановки. Итак, как можно решить систему линейных уравнений? Рассмотрим этот способ на примере системы трёх уравнений с тремя неизвестными. 

На первом этапе решения систему уравнений необходимо привести к трапециевидной форме, которая выглядит следующим образом:

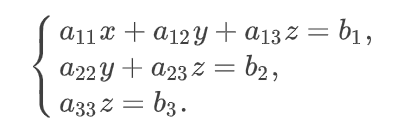
Для этого нужно провести несложные линейные преобразования с коэффициентами расширенной матрицы системы. Расширенная матрица системы отличается от матрицы системы лишь тем, что она содержит ещё и столбец правых частей уравнений, который записывается справа. Преобразования включают в себя сложение или вычитание строк матрицы, а также умножение элементов строки на число.

Применим данный метод к системе линейных уравнений с тремя переменными:

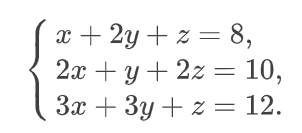
Расширенная матрица A данной системы принимает вид:

Проводя преобразования строк, нужно добиться того, чтобы в третьей строке расширенной матрицы на первом и втором местах были нули, а во второй строке — нуль на первом месте (возможно, при этом во второй строке будет ещё нуль и на третьем месте).

Вначале вычтем из второй строки матрицы первую строку, умноженную на два, в результате во второй строке окажется два нуля. Затем вычтем из третьей строки первую строку, умноженную на три, в результате чего в третьей строке окажется только один ноль:

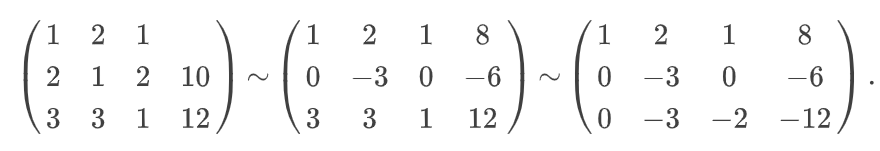
С одной стороны, можно остановиться на данном этапе, поменять вторую и третью строку местами, решить систему уравнений, соответствующую полученной расширенной матрице: 

С другой стороны, следуя алгоритму решения системы уравнений, необходимо вычесть из третьей строки расширенной матрицы вторую строку и получить два нуля в последней строке матрицы:

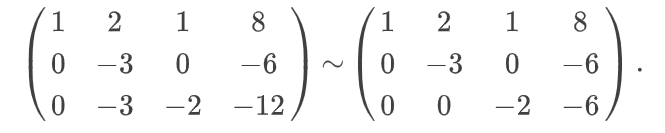
Это позволит перейти к решению ещё более простой системы линейных уравнений:

Теперь реализуем обратный ход метода Гаусса: из третьего уравнения системы определим z = 3 , из второго — y = 2. Далее используем метод подстановки и определим значение x:

Итак, решение системы линейных уравнений методом Гаусса: x = 1, y = 2, z = 3.

Ответы к пункту 24. Сравнение дробей, стр. 23

Объясните с помощью рисунка, почемуа) 1/3 = 4/12; б) 3/4=9/12

Решение

Задание № 92

Начертите в тетради отрезок длиной в 18 клеток. С помощью этого отрезка объясните, почему: а) 2/9 = 4/18; б) 5/6=15/18.

Решение

Задание № 93

Единичный отрезок равен 12 клеткам. Отметьте на координатном луче точки A(5/6) и B(10/12). Объясните результат.

Решение

Отметьте на координатном луче точки, координаты которых равны:а) 1/5,2/5,3/5,4/5;б) 1/8,3/8,5/8,7/8.

Ответ

Задание № 95

Единичный отрезок равен длине 6 клеток тетради. Отметьте на координатном луче точки с координатами 1/2;1/3;1/6;2/3. Какая из этих точек левее всех расположена на луче, а какая правее всех?

Решение

Задание № 96

Расставьте в порядке возрастания дроби:7/12; 1/12; 5/12; 9/12; 11/12; 4/12.Расставьте эти дроби в порядке убывания.

Решение

Oh My God!

В трейлере также появляется Мэгги Уилер — актриса, сыгравшая Дженис с противным голосом и ужасающим смехом, подругу Чендлера, с которой тот познакомился в интернете от отчаяния и от которой впоследствии никак не мог избавиться на протяжении всего сериала. Она появляется в 23 эпизодах. Даже в самом конце ситкома, когда Чендлер и Моника пытаются купить дом, за него сражается Дженис с мужем. Чендлеру приходится притвориться, что он до сих пор влюблен в Дженис, чтобы ее отвадить. Каждый раз, когда Дженис возникает в кадре, она произносит свою фирменную фразу: «О, мой бог!»

Многие думали, что у актрисы в принципе такой голос, но после интервью в шоу This Morning стало понятно, что она это очень хорошо сыграла. На самом деле у нее приятный тембр.

Пункт 33. Приближенные значения чисел. Округление чисел. Страница 83

Задание 420

Между какими соседними натуральными числами расположена каждая из дробей: 6,78; 83,74; 126,2? К какому из этих чисел дробь ближе?

Решение

Задание 421

Длина прямоугольника х см, а его ширина у см. Укажите приближённые значения с недостатком и с избытком для периметра и для площади этого прямоугольника, если:а) 7 < х < 8, 3 < у < 4;б) 20 < х < 25, 16 < у < 18.

Решение

Округлите до единиц дроби:7,265; 11,638; 0,23; 8,5; 300,499; 6,5108; 0,8.

Решение

Задание 423

Старинная русская мера массы пуд равна 16,38 кг. Округлите это значение до целых, до десятых. Старинная русская мера длины верста равна 1067 м. Округлите это значение до десятков, до сотен. Старинная русская мера длины сажень равна 2,13 м. Округлите это значение до целых, до десятых.

Решение

Умножение числа 3

Страница 36 — 37

1. Для каждого цыплёнка нарисуй по 3 зернышка. Сколько всего зёрнышек получилось? Заполни пропуски.

Решение:

                   3 + 3 + 3 + 3 + 3 = 3 * 5 = 15 (з.)

2. Обозначь на чертеже вершины каждого многоугольника буквами. Сколько тебе понадобилось букв? Запиши.

Решение:

Для обозначения многоугольников понадобилось 9 букв: А, В, С, О, 
М, Р, Т, Е, Х.

3. По данным точкам начерти незамкнутую ломаную АБСДЕ.

Измерь длину каждого звена и вычисли сумму.

Решение:

АБ + БС + СД + ДЕ =

4. Проверь, являются ли данные примеры круговыми. Если да, то соедини их линией так, чтобы ответ предыдущего примера был первым числом в следующем примере.

Решение:

5) Дополни схему и реши задачу. В одном сервизе 12 чашек, а в другом на 6 чашек меньше. Сколько всего чашек в двух сервизах.

Решение: 1) 12 — 6 = 6 (ч.) 2) 12 + 6 = 18 (ч.) Ответ: в двух сервизах 18 чашек.

6. В семье трое детей: два мальчика и девочка. Их имена начинаются с букв А, В, Г. Среди букв А и В есть начальная буква имени только одного мальчика. Среди В и Г есть начальная буква имени только другого мальчика. С какой буквы начинается имя девочки?

Решение:
    В условии задачи сказано, что среди букв А и В есть начальная 
буква имени только одного мальчика, значит вторая буква 
из А и В - это начальная буква имени девочки. 
    Методом исключения получаем, что имя второго брата - 
начинается с буквы Г.
    Также в условии задачи сказано, что среди В и Г есть 
начальная буква имени только другого мальчика.Так как мы 
выяснили, что имя второго мальчика начинается с буквы Г, то 
с буквы В начинается имя девочки. Соответственно с буквы
А начинается имя первого брата.

Ответ: имя первого брата называется с буквы "А", имя 
второго брата начинается с буквы "Г", имя девочки 
начинается с буквы "В".

Страница 38 — 39

1. На каждой тарелке нарисуй и раскрась по 3 огурца. Сколько всего огурцов нарисовано?

Огурцы на тарелке

Решение:

Тарелки с огурцами

3 + 3 + 3 + 3 = 12 огурцов.

2. В одной банке 3 кг краски. Сколько килограммов краски в 6 таких банках?

Банки с краской

3 + 3 + 3 + 3 + 3 + 3 = 3 * 6 = 18 кг.

3. Каждый чемодан соедини с его ручкой так, чтобы предложение и пример означали одно и то же.

Чемоданы

4. Сравни.

2 * 2 = 2 + 2       3 * 3 > 3 + 3       2 * 5 > 2 + 5
2 * 3 > 2 + 3       3 * 4 > 3 + 4       3 * 6 > 3 + 6
2 * 4 > 2 + 4       3 * 5 > 3 + 5       2 * 8 > 2 + 8

5. Кто первым забьёт гол в матче между командами «Квадраты» и «Треугольники»? Правила таковы: футболист может передать мяч только тому игроку, у которого номер на футболке равен ответу примера, записанного под данным футболистом. Например, игрок номер 7 передаст мяч футболисту под номером 6, так как 2 * 3 = 6. Нарисуй плавной линией схему передачи мяча от игрока к игроку. Забей мяч в ворота.

Матч по футболу

Мяч забил игрок команды «Треугольники! под номером 3.

6. Сравни.

14 кг > 4 кг          12 см > 1 дм         1 дм 3 см < 2 дм
18 л > 10 л           2 дм > 10 см         1 дм 7 см = 17 см

7. Любе 11 лет, Надя на 4 года младше Любы, а Вера на 7 лет старше Нади. Сколько лет Наде и сколько лет Вере? Запиши ответы.

Наде 11 - 4 = 7 лет.
Вере 7 + 7 = 14 лет.

Страница 40 — 41

1. Заполни пропуски в таблицах.

Таблица

2. Реши примеры с помощью числового луча.

Числовые лучи

3. Выполни вычисления. Расшифруй имя героини сказки, расположив ответы примеров в порядке увеличения.

Зашифрованное имя героини сказки

Зашифрованное имя героини сказки — Белоснежка.

4. Заполни пропуски, выполнив вычисления.

Заполнение пропусков

236 эпизодов американского ситкома до сих пор популярны и любимыми зрителями всех возрастов по всему миру

22 сентября исполнилось четверть века с выхода первого эпизода сериала «Друзья» от Warner Bros. Ситком заполучил поклонников по всему миру и вечную любовь телезрителей. Это подтверждает даже то, что Netflix в прошлом году купил у Warner Bros права на показ сериала за $100 млн.

Празднование юбилея началось с того, что знаменитый оранжевый диван, на котором друзья сидели в Central Perk, отправился в путешествие по всему миру. Фанаты получили возможность сфотографироваться с частью истории. Его тур продлится на протяжении всей осени, он будет стоять в Нью-Йорке рядом с Empire State Building, на площади Джексона в Новом Орлеане, а также в Лондоне, Мадриде и Лос-Анджелесе.

Телевизионные каналы и онлайн-кинотеатры в эти праздничные для фанатов «Друзей» дни предлагают своим зрителям насладиться бонусным контентом. Например, посмотреть кадры ситкома, которые на вышли на ТВ, а также эксклюзивные интервью с актерами и продюсерами.

Подготовил сюрприз фанатам и Google, который спрятал пасхалки с отсылками к телесериалу в свою поисковую систему. Для того чтобы увидеть их, необходимо вводить в поисковике имена главных героев, тогда рядом с их фотографиями появятся отличительные знаки: рядом с Джоуи — изображение пиццы, а рядом с Фиби — гитара, при нажатии на которую заиграет песня «Драный кот». Около Рейчел Грин будет изображение парика, а около Чендлера — офисное кресло.

Модный бренд Ralph Lauren, в котором некогда работала Рейчел, тоже выпустил специальную коллекцию к 25-летию шоу. Дизайнеры бренда при создании специальной коллекции черпали вдохновение в гардеробе Рейчел, воссоздав её пальто с леопардовым принтом, плиссированную кожаную мини-юбку, шерстяной блейзер и другие вещи.

Несколько недель назад производитель конструктора Lego посвятил сериалу новый набор. Конструктор увековечил любимую кофейню друзей, включая много знакомых фанатам вещей — оранжевый диван, синтезатор Росса, «мужская сумка» Джоуи, ноутбук Чендлера, гитара Фиби. Набор включает всю компанию друзей, в том числе Фиби, дебютирующую со своим самым большим хитом «Драный кот», Рейчел — официантку, Джоуи с его любимой пиццей. Есть даже крошечная фигурка Гюнтера.

А на Манхэттене открыли целый музей «Друзей», экспозиция которого состоит из комнат героев, кофейни Central Perk и фонтана из начальных кадров фильма. Посетителям можно сфотографироваться в интерьере, выпить кофе в Central Perk, а также посмотреть фото- и видеоматериалы о том, как создавался ситком. Там есть забавные экспонаты из любимых моментов «Друзей»: индейка, которую надела на голову Моника в День Благодарения; диван, который друзья пытались поднять наверх; манекены, которые показывают эволюцию причесок Рейчел в фильме. Есть у музея и сайт, на котором можно приобрести специальные сувениры.

Pottery Barn анонсировал коллекцию в честь 25-летия друзей, несмотря на то, что истинные фанаты сериала знают о нелюбви Фиби к этому массовому бренду. Компания выпустила аптекарский столик, который в шестом сезоне одновременно купили Рэйчел и Роуз, и другие предметы домашнего декора. Они включают кружки с надписью «Ты мой лобстер», подушечки и полотенца, напоминающие о сериале.

Сеть Coffee Bean & Tea Leaf совместно с Warner Bros предложила фанатам сериала разные брендовые продукты: от ограниченной партии кофейных зерен и чая до кружек из кофейни Central Perk.

Alex and Ani совместно с Warner Bros представил ограниченную партию браслетов с популярными фразами героев.

Главные герои ситкома также не могли забыть знаменательную дату: Кортни Кокс, Лиза Кудроу, Дэвид Швиммер и Мэтт Леблан одновременно опубликовали в Instagram один и тот же постер к одному из первых сезонов. Так они поблагодарили всех своих преданных поклонников по всему миру.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax2 + c = 0, при b = 0;
• ax2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax2 = 0.

Уравнение ax2 = 0 равносильно x2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x2 = 0 является нуль, так как 02 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6×2 = 0.

Как решаем:

1. Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

   −6×2 = 0

   x2 = 0

   x = √0

   x = 0

Ответ: 0.

Как решить уравнение ax2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax2 + c = 0:

• перенесем c в правую часть: ax2 = — c,
• разделим обе части на a: x2 = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а < 0, то уравнение x2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.

Если — c/а > 0, то корни уравнения x2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = — c/а. Ура, больше у этого уравнения нет корней.

В двух словах
Неполное квадратное уравнение ax2 + c = 0 равносильно уравнению х2= -c/a, которое: не имеет корней при — c/а < 0; имеет два корня х = √- c/а и х = -√- c/а при — c/а > 0.

Пример 1. Найти решение уравнения 8×2 + 5 = 0.

Как решать:

1. Перенесем свободный член в правую часть:

   8×2 = — 5

2. Разделим обе части на 8:

   x2 = — 5/8

3. В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8×2 + 5 = 0 не имеет корней.

Как решить уравнение ax2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

1. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

2. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax2 + bx = 0 имеет два корня:

• x = 0;
• x = −b/a.

Пример 1. Решить уравнение 0,5×2 + 0,125x = 0

Как решать:

1. Вынести х за скобки

   х(0,5x + 0,125) = 0

2. Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
3. Решить линейное уравнение:

   0,5x = −0,125,
   х = −0,125/0,5

4. Разделить:

   х = −0,25

5. Значит корни исходного уравнения — 0 и −0,25.

Ответ: х = 0 и х = −0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax2 + bx + c, то справедливо равенство ax2 + bx + c = a (x − x1) (x − x2).

Эпизод «Друзей» с покупкой дивана озадачил математика. Он доказал — мебель (и нервы Росса) можно было спасти

Математик вычислил, что Росс, Чендлер и Рэйчел могли поднять диван по лестнице в одном из эпизодов «Друзей», а не резать его пополам. В помощь горе-грузчикам — уравнение с теоремой Пифагора, которое поможет просчитать угол и спасти Чендлера от застревания, а Росса — от нервного срыва.

Одним из наиболее запоминающихся моментов культового ситкома «Друзья» стал эпизод, где Росс Геллер приобрёл новый диван и отказался платить магазину за доставку (5 сезон, 16 серия). В качестве грузчиков выступили друзья Росса Чендлер Бинг и Рэйчел Грин, которые поднимали покупку по лестнице в квартиру.

Росс разработал план, но мебель застряла в лестничном пролёте. Эпизод закончился на кадрах из магазина, где экономный герой возвращает диван, перерезанный пополам.

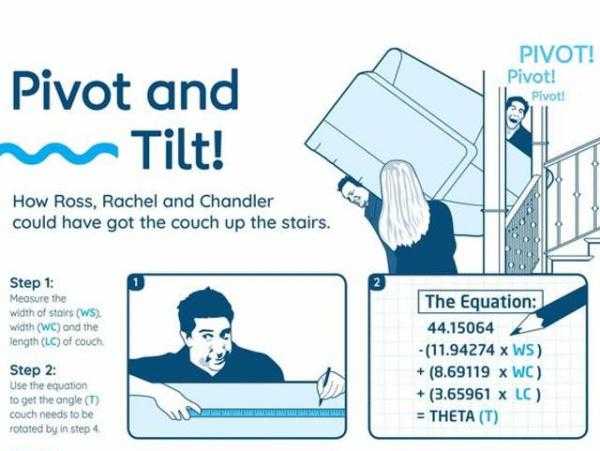
Проанализировав сцену, специалист в области точных наук Кэролайн Цункель раскрыл методологию и уравнение, которое, по его мнению, помогло бы закончить операцию по доставке дивана на «пять». Математик создал инфографику, включающую уравнения и визуальную демонстрацию, необходимую для перемещения.

Экспериментаторы провели более 10 тысяч симуляций, чтобы доказать: наклоняя и поворачивая диван определённым образом, Росс, Рэйчел и Чендлер могли подняться по лестнице. Основой для нового плана стало уравнение, с помощью которого можно вычислить минимальный уровень наклона, необходимого для поворота предмета под углом 90 градусов (именно так расположены перила на лестничной площадке).

Угол вертикального наклона (T) = 44,15064 -11,94274xWS (ширина лестничной клетки) + 8,69119xWC (ширина дивана) + 3,65961xLC (длина дивана).

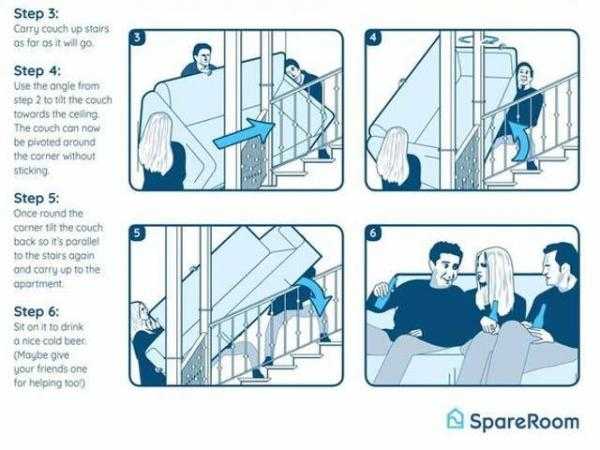
Напомним, что фанаты «Друзей» долгое время ждали спецвыпуск, где актёры обсудят десять лет, которые провели на площадке. Мечта исполнилась 27 мая, а с ней пришла и новая Фиби Буффе, которую точно оценят поклонники Леди Гаги.

А видео промо «Друзей» заставило зрителей вытереть горькие слёзы. Всё дело в Мэттью Перри, который, по мнению обитателей твиттера, перенёс тяжёлый недуг.

Справочная информация

ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной

Одарённая

Рейтинг	Кинопоиск — 7.9/ IMDB — 7.6
Жанр	Драма
Производство	США / 2017
Бюджет	$7 000 000
Сборы в мире	$43 046 590
Режиссёр	Марк Уэбб
В ролях	Крис Эванс, Маккенна Грейс, Линдси Дункан, Октавия Спенсер, Дженни Слейт, Майкл Кендалл Каплан, Джон М. Джексон, Гленн Пламмер, Джон Финн, Элизабет Марвел

«Одарённая» — потрясающий фильм про девочку математика. Фрэнк Адлер, бывший профессор философии Бостонского института, а нынче мастер по ремонту лодок, сам воспитывает свою семилетнюю одарённую племянницу Мэри в западной Флориде в качестве её фактического опекуна. Понимая её невероятные математические способности, он надеется, что она сможет жить нормальной жизнью и записывает Мэри в обычную государственную школу.

Когда мать Фрэнка, Эвелин, узнаёт об этом, она хочет забрать внучку и отдать её в частную школу для вундеркиндов в Бостоне. Во время битвы за опеку всплывут истории об отношениях между Эвелин, Фрэнком и Дайаной, покойной матерью Мэри.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)2- 4ac = 4n2 — 4ac = 4(n2- ac) и подставим в формулу корней:

Для удобства вычислений обозначим выражение n2 -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

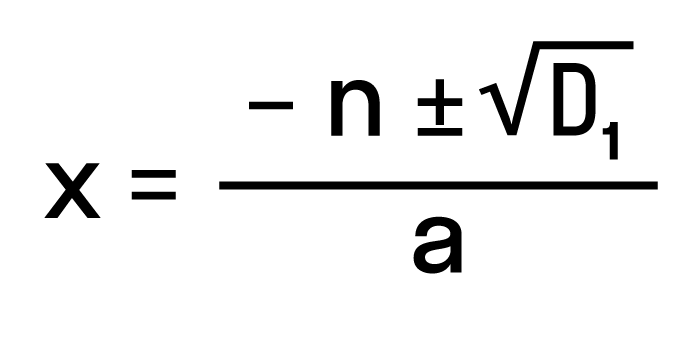
где D₁ = n2- ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

• вычислить D₁= n2- ac;
• если D₁< 0, значит действительных корней нет;
• если D₁= 0, значит можно вычислить единственный корень уравнения по формуле x = -n/a;
• если же D₁> 0, значит можно найти два действительных корня по формуле

Формулы арифметической прогрессии

В 9 классе проходят все формулы арифметической прогрессии. Давайте узнаем, какими способами ее можно задать:

1. Рекуррентной формулой:
2. Формулой n-го члена: a_n = a₁+ d · (n — 1).
3. Формулой вида a_n = kn + b, где k и b — числа, n — число членов последовательности.

Сумма первых n членов арифметической прогрессии (а_n) обозначается S_n:

Формулы нахождения суммы n членов арифметической прогрессии:

Чтобы быстрее запомнить формулы можно использовать такую табличку с основными определениями:

Рассмотрим пример арифметической прогрессии.

Дано: арифметическая прогрессия (a_n), где a₁ = 0 и d = 2.

Найти: первые пять членов прогрессии и десятый член прогрессии.

Решение арифметической прогрессии:

1. Чтобы найти последующий член прогрессии, нужно к предыдущему прибавить разность:

   a₂ = a₁ + d = 0 + 2 = 2;

   a₃ = a₂ + d = 2 + 2 = 4;

   a₄ = a₃ + d = 4 + 2 = 6;

   a₅ = a₄ + d = 6 + 2 = 8.

2. Используем общую формулу a_n = a₁ + d * (n — 1).

   По условиям задачи n = 10, подставляем в формулу:

   a₁₀ = a₁ + 2 * (10 — 1) = 0 + 2⋅9 = 18.

«Эпизод с бутербродом Росса» (5 сезон, 9 серия)

В пятом сезоне Россу пришлось многое сделать; он разводится во второй раз, его лучший друг спит с его сестрой, и ему негде жить. Все эти события привели к тому, что у него случился нервный срыв из-за, казалось бы, простого недоразумения: коллега съел его бутерброд, оставшийся на День Благодарения.

«Создатель влаги», как назвал это Росс, был очень важен для него, настолько важен, что заставил его наброситься на своего босса. В свою очередь, Росс был отправлен в творческий отпуск и вынужден разбираться со своими действиями, что для него означало поедание сладкой ваты в Центральной кофейне. Это был забавный взгляд на тяжелое время для Росса, и перерыв в работе, вероятно, был в его интересах.

Пункт 36. Умножение десятичных дробей. Страница 104

Задание 541

Найдите площадь прямоугольника со сторонами 12,5 дм и 6,2 дм. Решите эту же задачу, переводя дециметры в сантиметры.

Решение

Задание 542

Выполните умножение:а) 354,2 * 0,1;б) 248,34 * 0,1;в) 3788,2 * 0,001;г) 2,8 * 0,1;д) 4,5 * 0,01;е) 0,08 * 0,1;ж) 54 * 0,001;з) 37 * 0,0001;и) 0,01 * 0,0001.

Решение

Задание 543

Длина пола 6,35 м, а его ширина 4,82 м. Чему равна площадь пола? Ответ округлите до десятых долей квадратного метра.

Решение

Задание 544

При посеве редиса расходуют 0,55 кг семян на один ар. Сколько килограммов семян редиса потребуется для посева на участке площадью 4 а; 0,1 а; 2,3 а; 1,5 а; 0,8 а; 1 га?

Решение

Скорость поезда 85 км/ч. Сколько километров пройдёт поездза 5 ч; за 0,1 ч; за 3,8 ч; за 1,5 ч; за 0,4 ч?

Решение

Масса 1 см³ железа равна 7,9 г. Найдите массу железной детали объёмом 3 см³ ; 0,1 см³ ; 4,9 см³ ; 0,5 см³.

Решение

Задание 547

Верёвку разрезали на две части. Длина одной части 5,4 м, а другая часть в 2,5 раза больше. Найдите первоначальную длину всей верёвки.

Решение

Задание 548

Выполните умножение:а) 6,25 * 4,8;б) 85,8 * 3,2;в) 74 * 4,9;г) 12,6 * 7,8;д) 0,8 * 0,92;е) 2,5 * 0,37;ж) 3,43 * 0,12;з) 0,25 * 0,48;и) 1,15 * 0,07;к) 6,023 * 5,6;л) 8,4 * 18,478;м) 2,749 * 0,48.

Решение

Задание 549

Запишите выражение:а) произведение суммы чисел а и 3,1 и числа b;б) сумма произведения чисел 4,1 и х и числа 8,65;в) разность произведений чисел 7,8 и m и чисел 0,45 и n;г) произведение суммы чисел a и b разности чисел c и d.

Решение

Прочитайте выражение:а) (а + 9,7) * (b − 3,61);б) 6,5mт − 7,6n;в) 0,8x + 0,9у;г) (m − n)(р + k).

Решение